QCM: Почему измерение на обертонах имеет значение

Распространенные системы контроля качества измеряют фундаментальные изменения резонансной частоты, а иногда и сопротивление, которое может каким-то образом быть связано с диссипативными свойствами пленки или среды.

Усовершенствованные системы, основанные на измерениях импеданса или понижающего сигнала, дают доступ к истинной диссипации, половине полосы пропускания или коэффициенту качества и позволяют проводить измерения на нескольких обертонах. Количество допустимых обертонов зависит от полосы пропускания прибора и от основной резонансной частоты кварца.

Порядок обертонов должен быть нечетным (1, 3, 5...), чтобы обеспечить антисимметричный характер движения кварца. Если порядок обертонов четный (2, 4, 6...), то деформация симметрична и ток между электродами отсутствует.

BluQCM QSD может измерять до 13-го обертона с помощью кварцевых кристаллов частотой 5 МГц. С помощью высокочастотных датчиков частотой 50 МГц можно измерить только 3-й обертон.

На рисунке ниже показано колебательное движение кварца на основной частоте f0 (вверху) и третьей гармонике 3f0 (внизу).

 

 

Зачем измерять обертоны или гармоники?

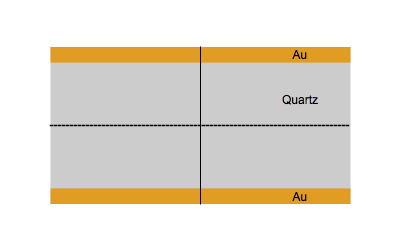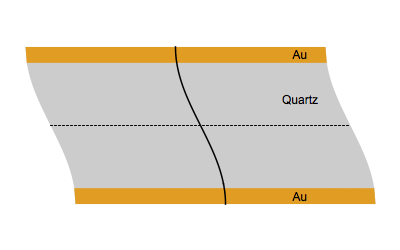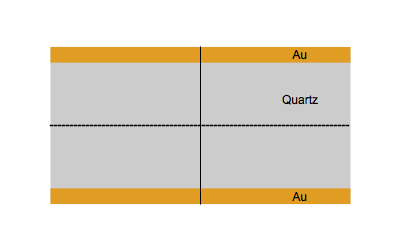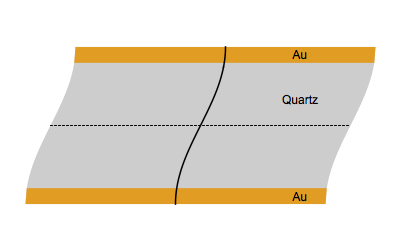
Измерение на гармониках дает еще один способ убедиться в том, что пленка, покрывающая оголенный электрод, является жесткой. Если значение Δfn/n является постоянным для каждой гармоники, пленку можно считать жесткой.

Измерения на обертонах более надежны

Значение Δfn/n, где fn - резонансная частота на n-й гармонике, теоретически должно быть постоянным в зависимости от порядка гармоник. Однако было отмечено, что она была постоянной только после 3-й гармоники, что тогда можно считать более надежным измерением изменения резонансной частоты. Это видно на рисунке отображенном ниже.

 

 

Измерения на гармониках необходимы для расширенной интерпретации данных

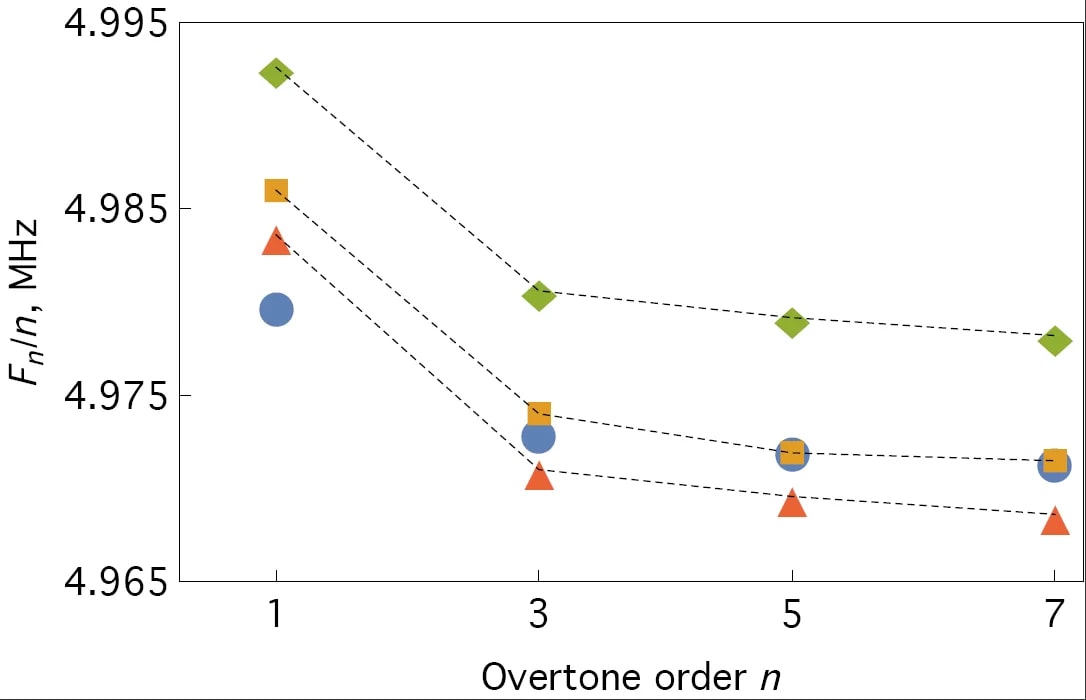
Диссипация и сдвиг резонансной частоты необходимы на нескольких гармониках, когда необходимо изучить и охарактеризовать вязкоупругие однородные тонкие пленки, частицы, молекулы или конформацию.

До тех пор, пока исследуемым объектом является рост или осаждение жесткой тонкой пленки, тонкой пленки Зауэрбрея или эластичной пленки, механический отклик не зависит от частоты. Это не тот случай, когда объектом исследования является вязкоупругая пленка, то есть пленка, в которой энергия волны одновременно упруго передается и вязко рассеивается. В этом случае отклик системы, состоящей из кварца, электродов, пленки и среды (воздуха или жидкости), зависит от входной частоты.

Можно провести параллель между электрической передаточной функцией системы, например, полным сопротивлением, и механической передаточной функцией системы, например, модулем сдвига. Точно так же, как импеданс Z(ω) (при ω=2nf) позволяет рассчитать отклик по току от входного потенциала, модуль сдвига G(ω) позволяет рассчитать отклик по напряжению от входного напряжения деформации. В вязкоупругой пленке модуль сдвига является сложной функцией, зависящей от частоты.

G(ω)=Re(G(ω))+jIm(G(ω))

Обертоны и гармоники - схожие термины, хотя кажется, что обертоны в основном используются в области акустики. Более того, в то время как “гармоники” означают несколько целых чисел основной частоты, включая основную частоту, “обертоны”, по-видимому, означают любое число, кратное основной частоте и превышающее ее, исключая основную частоту