Принципы измерения кварцевых микровесов

QCM: Принципы измерения

Микровесы из кварцевого кристалла основаны на том факте, что резонансная частота кварцевого резонатора изменяется при изменении его толщины. Используя уравнение Зауэрбея, мы можем рассчитать изменение массы по этому изменению частоты. 

Существует несколько методов, используемых для измерения резонансной частоты и мониторинга изменений резонансной частоты. Стандартный исторический метод, использующий генераторные схемы, ограничен измерениями резонансной частоты на основной частоте, в то время как усовершенствованные системы, использующие анализ импеданса или понижающий сигнал, обеспечивают измерение рассеяния и обертонов. Хороший обзор этих методов дан на стр. 23 в книге Д. Йоханнсмана.

В этой статье мы опишем только метод анализа импеданса, используемый в BluQCM. Зная номинальную резонансную частоту данного резонатора, BluQCM выполняет измерение импеданса или, скорее, пропускной способности на частотах, близких к номинальной резонансной частоте. Построив график действительной части пропускания, также известной как восприимчивость, в зависимости от частоты, мы получим кривую. Также, на рисунке ниже проиллюстрирован эффект увеличения толщины резонатора: при увеличении толщины резонансная частота смещается к более низким значениям, как предсказывает уравнение 3 в книге Quartz Crystal Microbalance: принципы и история.

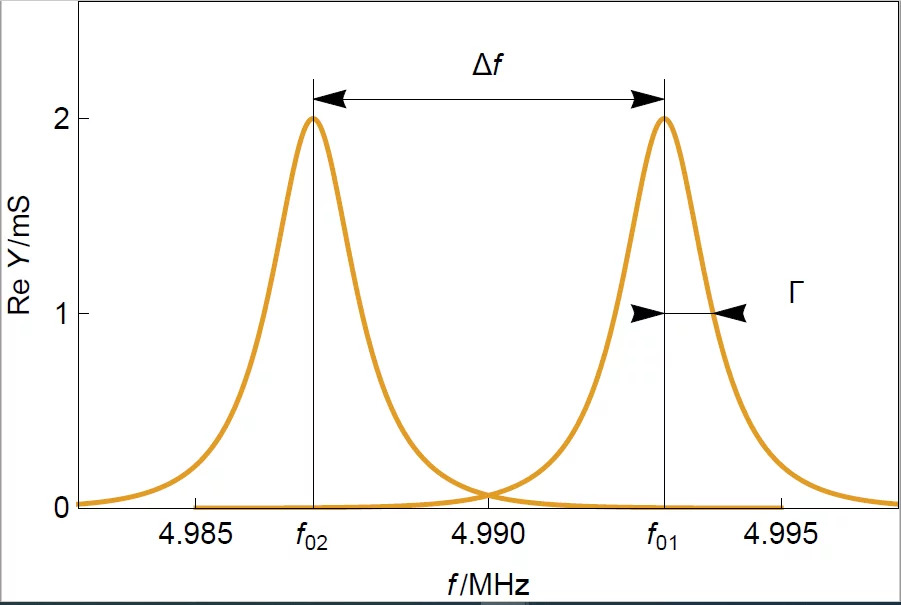
Добавление жесткого слоя, который, как предполагается, является эластичным, чтобы двигаться так же быстро, как кварц, т.е. обладать теми же механическими свойствами, что и кварц (тот же модуль сдвига и плотность), имеет тот же эффект, что и увеличение толщины кристалла: сдвигается резонансная частота и ширина полосы пропускания, хотя константа изменяется незначительно.

 

На резонансной частоте пропускная способность максимальна, что означает, что амплитуда колебаний кварца также максимальна. Также можно видеть, что пик имеет определенную ширину, показывающую дисперсию резонансной частоты кварца. Коэффициент Γ - это полуширина при половинном максимуме, также называемая половинной полосой пропускания.

Ширина полосы пропускания связана с упругими свойствами резонатора, а также со средой, в которой вибрирует кристалл.

Как указывалось ранее, измерение BluQCM представляет собой измерение импеданса или, скорее, пропускной способности, выполняемое между двумя электродами резонатора. Поскольку резонатор выполнен из пьезоэлектрического материала, реакция системы на электрическую модуляцию является не только электрической, но и вибрационной или акустической. Однако система может быть смоделирована с помощью простой эквивалентной схемы, которая называется эквивалентной схемой Баттерворта-ван Дайка (BvD):

Электрические компоненты в верхней ветви, которая называется двигательной ветвью, имеют эквиваленты в качестве двигательных компонентов. Нижняя ветвь называется электрической ветвью. Резонансная частота - это частота, для которой Im(Y)=0

Взаимосвязь между резонансной частотой и половиной полосы пропускания с компонентами схемы BvD следующая:

1. 
2. 

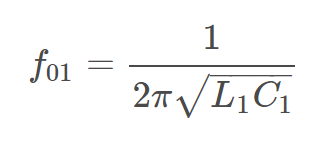
Γ - это прямое измерение дисперсии резонансной частоты в Гц и это напрямую связано с акустическими свойствами пленки. Этот параметр необходимо измерить, чтобы иметь возможность убедиться в том, что уравнение Зауэрбрея может быть применено для определения изменения массы по изменению частоты.

Стандартные приборы обычно показывают только изменения резонансной частоты и сопротивление R1, из которых можно определить полосу пропускания или рассеяние D без единицы измерения:

• 

 

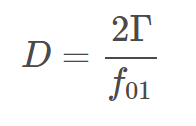
Эти измерения выполняются на основной резонансной частоте, но с помощью BluQCM (https://ilpa-tech.ru/produktsiya/kvartsevyj-mikrobalans/131-bluqcm-qsd) их можно выполнять на гармонических частотах или обертонах. Выполнение измерений на обертонах позволяет пользователям проверить правильность уравнения Зауэрбрея. Резонансные частоты и измерения рассеяния на обертонах позволяют также охарактеризовать вязкоупругие тонкие пленки, частицы, молекулы или даже их конформацию.